Dr. Stefan Lang am 21. Dezember 2018
Klinische Doktorarbeit und Statistik – wer ist Kaplan-Meier?
Möchte man eine Arbeit zu einer klinische Studie schreiben, hat man es oft mit Überlebenszeitanalysen von behandelten und unbehandelten Patienten zu tun. Darstellen kann man diese Analysen mit Kaplan-Meier-Kurven. Das sind treppenähnlichen Diagramme, die eigentlich gar keine richtigen Kurven sind. Was genau bedeuten sie?
In klinischen Studien möchte man oft wissen, wie lange es dauert bis ein bestimmtes Ereignis eintritt bzw. ob durch eine bestimmte Behandlung die Zeit bis zu diesem Ereignis verlängert werden kann.
Dabei muss es nicht immer ein negatives Ereignis sein (Todesfall). Es kann auch etwas Positives sein (Geburt, Heilung). Trotzdem spricht man in beiden Fällen von der Überlebenszeitanalyse.
Überlebenszeitanalysen werden in einer klinischen Doktorarbeit oder einer biomedizischen Publikation meist mit Kaplan-Meier-Kurven dargesetellt.
Problem bei Überlebenszeitanalysen
Das Problem ist, dass die Beobachtungszeit für die untersuchte Population nicht immer die gleiche ist.
Zum einen kann man eine klinische Studie nicht bis ultimo in die Länge ziehen. Daher wird das Ereignis bis Studienende nicht bei allen Teilnehmern eingetreten sein. Für diese kann man also keine exakte Überlebenszeit angeben – nur einen Mindestwert.
Zum anderen verlassen Patienten gelegentlich eine Studie aus ganz verschiedenen Gründen. Manche erscheinen vielleicht einfach nicht mehr zum nächsten Termin (lost to follow up), andere sind vielleicht bei einem Verkehrsunfall, also einem anderen („konkurrierenden“) Ereignis ums Leben gekommen. Die Beobachtungszeit endet, bevor das Ereignis eingetreten ist (dazu sagt man: „zensiert“).
Wichtig: Im Gegensatz zu manch anderen Verfahren verbleiben die „zensierten“ Beobachtungszeiten in der Analyse, denn schließlich verraten diese Daten, dass die Teilnehmer mindestens bis zu ihrem Ausscheiden aus der Studie überlebt haben.
Da also die Beobachtungszeit nicht immer die gleiche ist, werden bei der Kaplan-Meier-Kurve Zeitintervalle betrachtet. Die Überlebenswahrscheinlichkeit wird für jedes Zeitintervall berechnet und bezieht sich auf die Patienten, die zu Beginn noch am Leben waren (das nennt man „bedingte“ Wahrscheinlichkeit).
Wie kann man die Überlebenswahrscheinlichkeit für seine Doktorarbeit berechnen?
Grob gesagt teilt man in jedem Zeitintervall die Zahl der überlebenden Patienten durch die Zahl der Patienten „unter Risiko“ (also Gesamtzahl zu Beginn des Intervalls). Ist also von anfänglich 20 Patienten in jedem Zeitintervall jeweils einer verstorben, sind das für das für die jeweiligen Zeitintervalle [1] 19/20, [2] 18/19, [3] 17/18 usw.:
[1] 0,95, [2] 0,947, [3] 0,944, [4] 0,941 etc.
Diese „bedingten“ Wahrscheinlichkeiten werden nun multipliziert, um die Überlebenswahrscheinlichkeit zu erhalten, also:
0,95 x 0,947 — 0,95 x 0,947 x 0,944 — 0,95 x 0,947 x 0,944 x 0,941.
Das sind dann:
0,899, 0,849 und 0,799.
Genauso verfährt man für die andere Gruppe.
Wie sieht das in der Kaplan-Meier-Kurve aus?
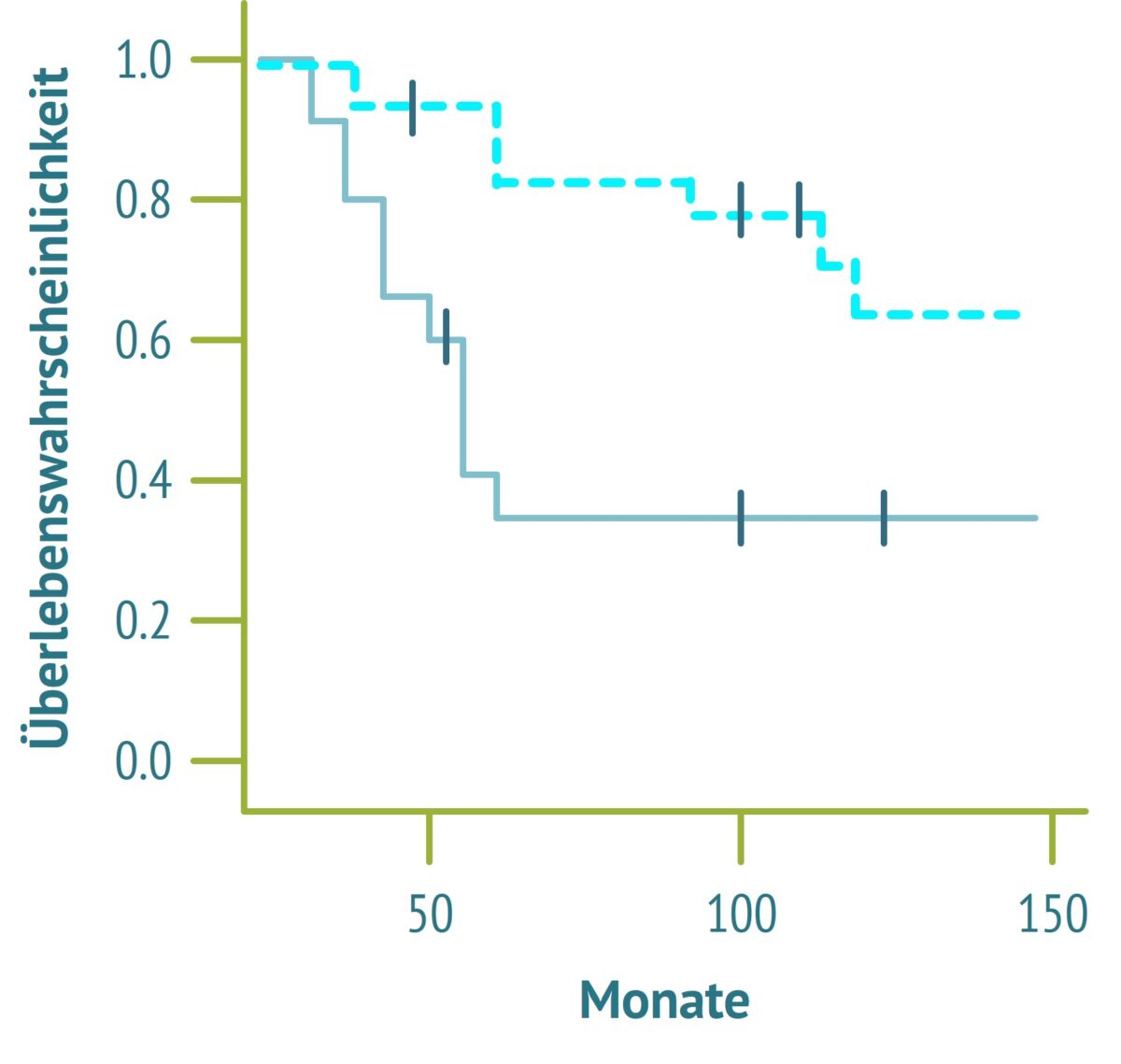
- Überlebenskurven (Kaplan-Meier) beginnen mit dem Beginn der Beobachtung und somit mit allen beobachteten Lebenden. Die bedingte Wahrscheinlichkeit ist daher 1,0.
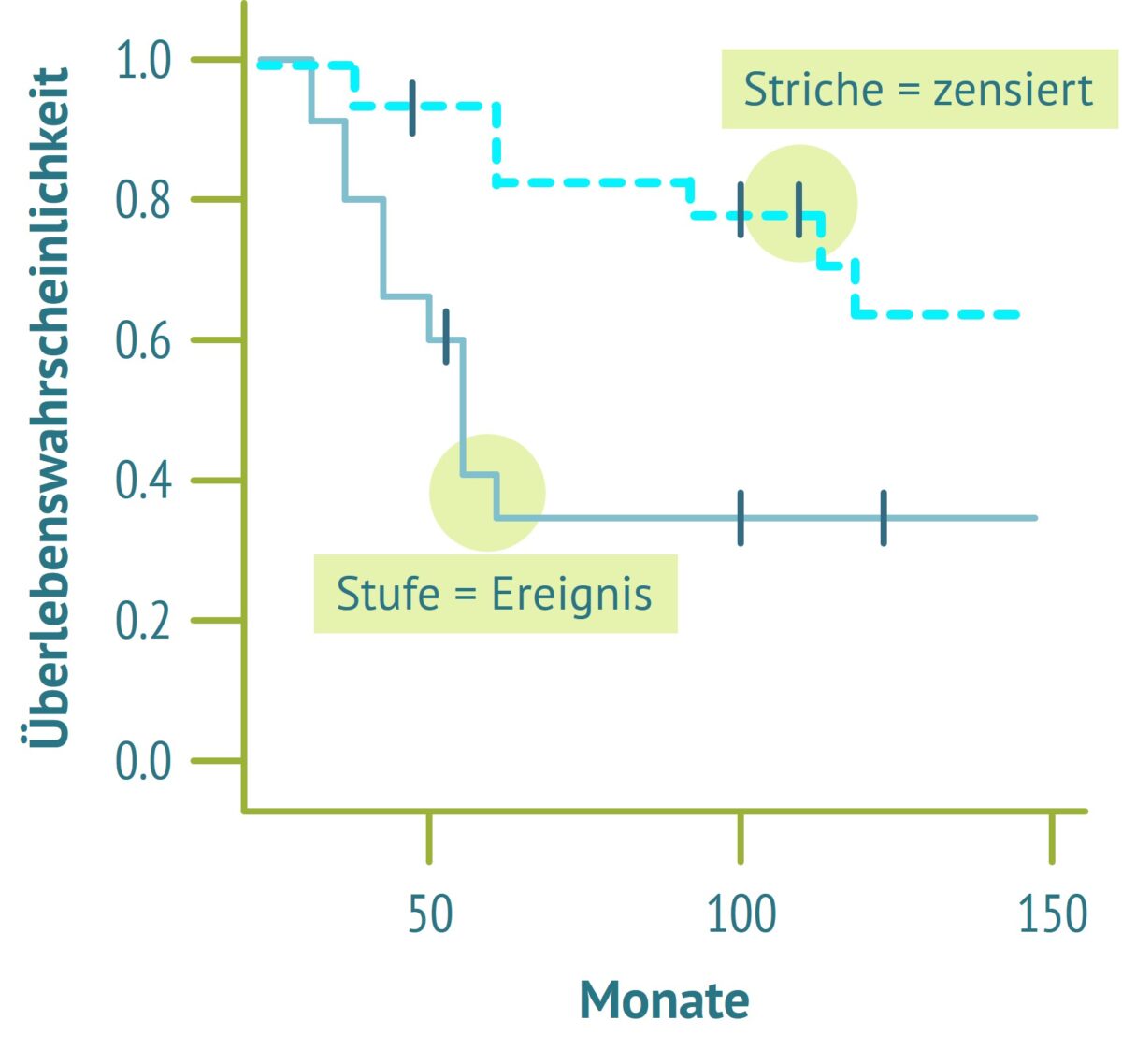
- Jeder Todesfall erniedrigt die Überlebenskurve. Das führt zu den klassischen „Stufen“. Die Treppenstufen sind dort, wo das untersuchte Ereignis eingetreten ist. Die Stufenhöhe entspricht der Zahl der Todesfälle.
- Zusätzlich werden zensierte Beobachtungen als vertikale Striche eingetragen. Sie zeigen an, wann der Beobachtungszeitraum für den entsprechenden Patienten endete.
- Eine steil abfallende Kurve sind also viele und frühe Todesfälle, eine flach verlaufende Überlebenskurve dagegen späte und wenige.
- Man erkennt klar, ob sich die Überlebenswahrscheinlichkeiten der beiden Gruppen im Studienverlauf unterschieden.
Statistik in Doktorarbeit oder Publikation: offene Fragen?
Ähnliche Themen rund um klinische Studien und die Statistik in einer wissenschaftlichen Publikation habe ich hier im Blog bereits behandelt:

