Dr. Stefan Lang am 04. September 2017

Statistik: Standardabweichung oder Standardfehler nach Gusto?

Kategorie Statistik

Ein Kollege gab mir mal den nicht ganz ernst gemeinten Rat: „Wenn die Unterschiede zwischen den Versuchsansätzen klein sind, nimm für deinen Fachartikel den Standardfehler SEM und hoffe, dass deine Leser denken, es wäre die Standardabweichung SD.“

In der Tat sieht der mittlere Fehler (standard error [SE]) kleiner aus als die Standardabweichung (standard deviation [SD]). Aber SE und SD unterscheiden sich grundlegend und man darf nicht einfach das eine gegen das andere austauschen. Denn das wäre Kosmetik.

Vor allem muss man im Text seiner Doktorarbeit oder seines Originalartikels klar benennen, was die Zahl hinter dem „±“ bedeutet: SE oder SD?

Standardabweichung und Standardfehler sind nicht das Gleiche

SD und SE unterscheiden sich grundlegend. Die Standardabweichung SD gibt die Streuung an – also um wie viel sich die einzelnen Werte voneinander unterscheiden. Das ist die durchschnittliche Entfernung aller gemessenen Werte vom Durchschnitt.

Der mittlere Fehler SE drückt dagegen aus, wie gut man den wahren Mittelwert kennt, also in welchem Maß der Mittelwert einer Stichprobe vom tatsächlichen Mittelwert in der Grundgesamtheit abweicht.

  • SD: Streuung der Werte einer Stichprobe (Streubreite)
  • SE: Genauigkeit des Mittelwerts einer Stichprobe (Genauigkeit des Mittelwerts)

Einfache Umrechnung

In der Statistik lassen sich SD und SE problemlos ineinander umrechnen:

SD = SEM x Wurzel aus n (Stichprobenumfang).

Beträgt der SE von 24 Proben 0,2, dann ist der SD mit 0,98 deutlich größer (0,2 x 4,89)., sodass der SE im Balkendiagramm tatsächlich „schöner“ aussieht. Doch in der Statistik etwas zu „schönen“ ist nicht zulässig.

Und was nehme ich nun für die Fehlerbalken?

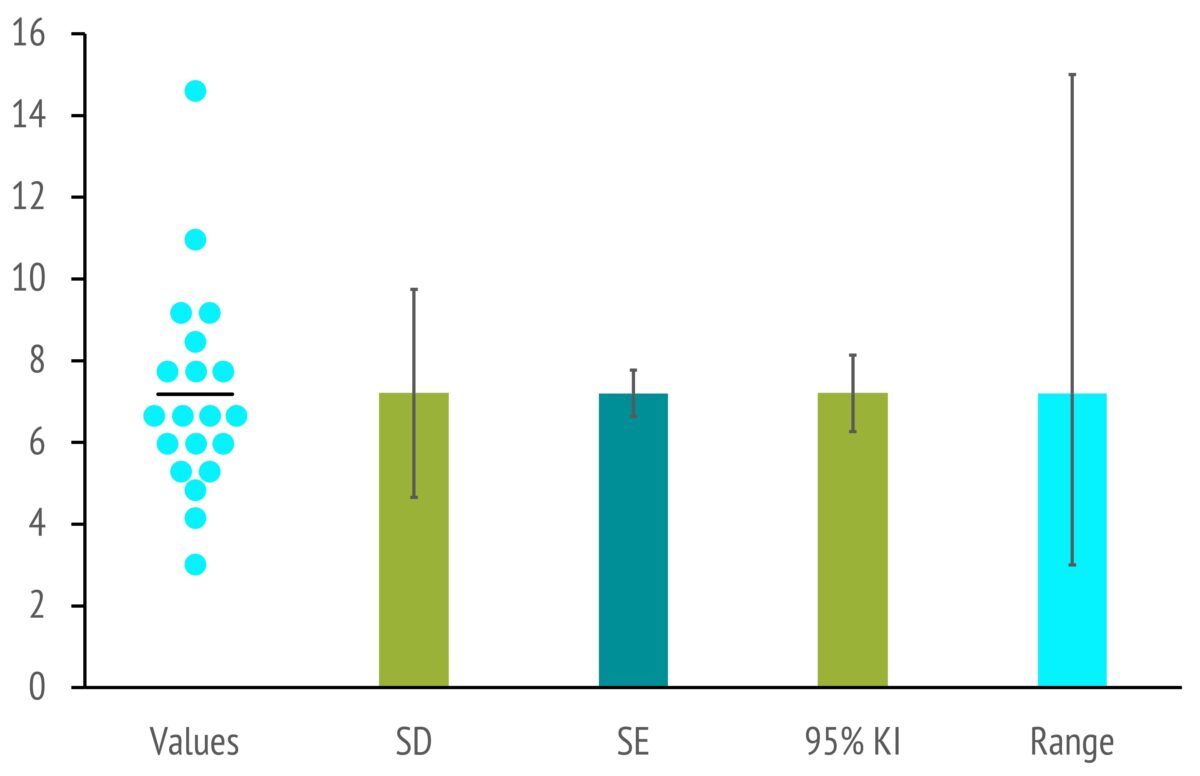
Fünf Möglichkeiten den Mitellwert mit seiner Streuung in der Statistik darzustellen.

SD für gestreute Einzelwerte

  • SD: Wenn man viele Einzelwerte hat, möchte man gewöhnlich die Streuung dieser Werte angeben. Mit dem Mittelwert ± SD kann man das sehr übersichtlich tun. Daher gehört der Mittelwert ± SD zu den häufigsten Varianten.
  • Values: Das könnte man auch mit einem Scatter-Plot tun, der ja die tatsächlichen Werte zeigt und somit die Streuung bildlich darstellt („Values).

SE für den Vergleich von Mittelwerten

  • SE: Wenn man dagegen Mittelwerte vergleichen möchte (z.B. mit dem t-Test), möchte man zeigen, wie präzise der jeweilige Mittelwert tatsächlich erhoben werden konnte. Dafür ist der Standardfehler gedacht (daher hängt der SE auch von dem Stichprobenumfang und vom SD ab).

Kofidenzintervall: Wertebereich

  • 95% KI: Das Konfidenzintervall ist ein Wertebereich, der einen bestimmten Parameter (zum Beispiel eine Mittelwert) mit einer vorab definierten Wahrscheinlichkeit enthält (meist 95 %).

Range

  • Range: Manchmal braucht man nur Mittelwert und Bandbreite, den Range.

Fünf Varianten für den Fachartikel und die Doktorarbeit

Entscheiden Sie, was Sie in Ihrem Fachartikel oder in Ihrer Doktorarbeit zeigen möchten, also einen Scatter-Plot mit den Einzelwerten, den Mittelwert ± SD, den Mittelwert ± SEM, das Konfidenzintervall oder auch den Mittelwert mit den entsprechenden Minimal- und Maximalwerten (Range).