Dr. Stefan Lang am 13. November 2023
Daten in der Doktorarbeit: Was ist der Mittelwert wert?
Wenn Elon Musk in Ihre Nachbarschaft zieht, steigt das mittlere Einkommen an Ihrem Wohnort ins Unermessliche – aber Sie verdienen trotzdem keinen Cent mehr. Der nackte Mittelwert in einer Doktorarbeit genügt also nicht.
Angenommen, Sie wohnen in einem kleinen Dorf. Alle fünf Haushalte verdienen pro Monat zwischen 2.400 € und 2.800 €. Eines Tages zieht ein Schwerverdiener mit einem Monatseinkommen von 1.500.000 € in Ihr Dorf. Was passiert mit dem mittleren Monatseinkommen der Dorfbewohner?
Mittelwert und seine möglichen Verzerrungen in der Doktorarbeit
Vergleichen Sie in Ihrer Doktorarbeit das monatliche Einkommen der Dorfbewohner zu zwei Zeitpunkten allein auf der Basis des Mittelwertes, dann erleben Sie eine Überraschung: Alle sind übernacht schwer reich geworden. Ein Blick in den eigenen Geldbeutel zeigt Ihnen jedoch: So kann das nicht stimmen.
Der nackte Mittelwert genügt für Ihre Doktorarbeit also nicht. Er ist viel zu anfällig für Verzerrungen und Fehlinterpretationen (für Ihre medizinische Doktorarbeit können Sie anstelle der Eurobeträge auch jeden anderen Parameter einsetzen).
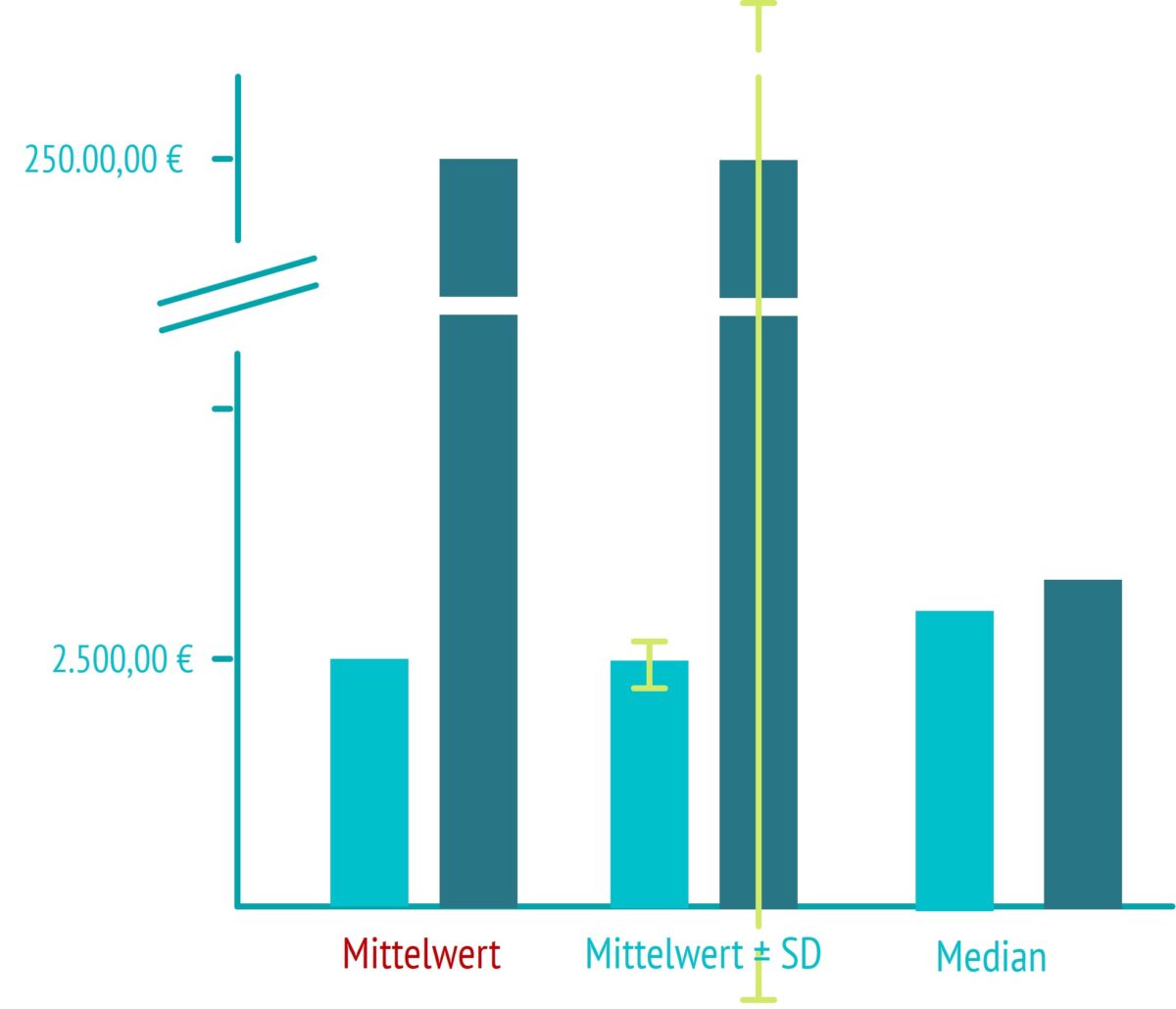
- Not good: „… zeigte sich ein Anstieg des mittleren Einkommens von 2.500 € auf 252.083 € …“
Bandbreite darstellen: Mittelwert mit Standardabweichung oder Range
Notwendig ist also, die Bandbreite der Werte anzugeben. Denn nur so verstehen die Leser Ihrer Doktorarbeit, wodurch dieser vermeintliche Anstieg zustande kam.
Dafür gibt es verschiedene Möglichkeiten. Die einfachsten sind die absolute Bandbreite oder die Standardabweichung. Die sehr hohe Standardabweichung zeigt Leser und Leserin übrigens, dass der gefundene Anstieg des mittleren Einkommens überhaupt nicht aussagekräftig und relevant ist.
- Good: “ … zeigte sich ein Anstieg von 2.500 € (Range: 2.400-2.800) auf 252.083 (2.400-1,500.000) …“
- Good: “ … zeigte sich ein Anstieg von 2.500 +/- 282 € auf 252.083 +/- 558.085 € …“ (Mittelwert +/- SD)
Robust gegen extreme Abweichungen: Median
Eine andere Möglichkeit, mit Daten umzugehen, die extreme Ausschläge zeigen: der Median. Im Gegensatz zum Mittelwert ist der Median sehr robust gegen Ausreißer. Dazu hatte ich bereits einen Blogbeitrag.
Verwenden Sie in Ihrer medizinischen Doktorarbeit für das Beispiel den Median anstelle des Mittelwertes, sieht man als Leser oder Leserin sofort, dass es eigentlich keinen relevanten Anstieg des Einkommens im Durchschnitt gab. Als Zusatz-Info kann man hierzu zum Beispiel noch die 1. und 3. Quartile als Maß der Bandbreite angeben.
- Good: „Das mediane Einkommen blieb unverändert (2.600 € vs. 2.650 €).“
- Good: „Das Einkommen (Median; Q1, Q3) im ersten Jahr (2.600 €; 2.200, 2.750) änderte sich im Folgejahr nicht (2.650 €; 2.300, 377.100)